题意:投一枚硬币向上的概率是q/p。问你投K枚硬币,向上的枚数为偶数枚的概率是?
要求的即为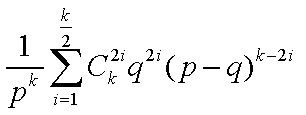 。
。
这个东西是个二项展开式的偶数项系数和,来,我们复习一下高中数学,设f(x)=(ax+b)^n,则其偶数项系数和为(f(1)+f(-1))/2。
#includeusing namespace std;typedef long long ll;#define MOD 1000000007llint T;ll p,q,K;ll Quick_Pow(ll a,ll p,ll mod){ if(!p){ return 1ll; } ll res=Quick_Pow(a,p>>1,mod); res=res*res%mod; if((p&1ll)==1ll){ res=(a%mod*res)%mod; } return res;}int main(){ //freopen("b.in","r",stdin); scanf("%d",&T); for(;T;--T){ scanf("%lld%lld%lld",&p,&q,&K); printf("%lld\n",(((Quick_Pow(p,K,MOD)+Quick_Pow(p-2ll*q,K,MOD))%MOD*Quick_Pow(2ll,MOD-2ll,MOD))%MOD *Quick_Pow(Quick_Pow(p,K,MOD),MOD-2ll,MOD))%MOD); } return 0;}